Iterators: Navigating Vectors Without the Need for Loops

In this blog post, we cover one of the most advanced and challenging concepts in the KDB/Q programming language: Iterators (formerly known as Adverbs). In grammar, an adverb is described as "a word that modifies or describes a verb, an adjective, another adverb, or even a whole sentence" [1]. Similarly, in KDB/Q, adverbs - or as they’re now called, iterators - or as they’re now called, iterators - are higher-order functions that modify how other functions are applied to lists. As someone passionate about finance, I like to think of them as derivatives, as they derive new functionality from the underlying function.

In 2018, the terminology in KDB/Q evolved, and from January 2019, the term "Iterators" officially replaced "Adverbs." If you’re looking to master Iterators in KDB/Q, there’s no better resource than the white paper on the topic by Conor Slattery and Stephen Taylor, which you can find here. I highly recommend reading it thoroughly. That said, I will also share my own thought processes and insights to help you understand the power of Iterators in KDB/Q more effectively.

Iterators can be broadly categorized into two main categories: Maps and Accumulators. In the following sections, we will explore each category and its corresponding iterators in detail, explaining their functionality and providing illustrative examples.

Why we use Iterators

Before diving into the powerful concept of Iterators and their applications, let’s take a moment to understand why they are such a game-changing tool and why we should use them. If you’ve worked with traditional object-oriented programming languages, you’re probably familiar with one of the most common beginner mistakes: the infamous IndexOutOfBoundsException. This error happens when you try to access an element in a list or array using an index that doesn’t exist - often caused by an error in loop logic.

In KDB/Q, this issue simply doesn’t happen. Iterators not only eliminate the need to manually track indexes, but they’re also significantly faster than traditional loops. Imagine how tedious and time-consuming it would be to write loops - or worse, nested loops - every time you needed to iterate over a list or a list of lists. With Iterators, these challenges disappear, allowing you to focus on the logic rather than wrestling with boilerplate code. It’s efficient, clean, and a joy to work with.

Don’t believe me? Let’s take a look at a simple example. Let’s say we have a list of strings representing fruits we eat, and we want to prepend each fruit’s name with a sentence. It’s a simple, beginner-level exercise. In Python, achieving this requires several lines of code - even though there might be shorter or more efficient methods (I’ll admit, I’m not a Python developer).

Python code:

fruits = ["apple", "banana", "cherry"]
for i in range(len(fruits)):
  print("The fruit I ate was a",fruits[i])

Output:

The fruit I ate was a apple
The fruit I ate was a banana
The fruit I ate was a cherry

Now, in KDB/Q, this task is effortlessly handled with Iterators. It’s built into the language, allowing you to accomplish it with unmatched simplicity. This demonstrates the paradigm shift that KDB/Q brings to the table - a change in the way you think and approach programming problems. To borrow a quote from Alan Perlis:

"A language that doesn't affect the way you think about programming is not worth knowing."

Above example in KDB/Q [using the each-right iterator]:

q)"The fruit I ate was a ",/:("apple";"banana";"cherry")
"The fruit I ate was a apple"
"The fruit I ate was a banana"
"The fruit I ate was a cherry"

Implicit Iteration

If you thought that was impressive, hold on tight - there’s even more. As a vector-oriented programming language, KDB/Q introduces the concept of implicit iteration. While a full explanation of this concept goes beyond the scope of this blog post, I highly recommend checking out Stephen Taylor's excellent write-up for an in-depth understanding. For now, let’s take a brief look at what implicit iteration entails:

The simplest form of implicit iteration occurs when working with two lists of the same length and applying an operation to them - such as adding them together. In most traditional programming languages, you would need to write a loop to iterate through the elements of both lists and add the numbers pairwise. In KDB/Q, however, this implicit map iteration is built in and works seamlessly right out of the box.

q)10 20 30+1 2 3
11 22 33

But that's not all - implicit iteration in KDB/Q also extends to lists of lists. While most traditional programming languages would require you to write nested loops to handle such cases, KDB/Q eliminates that need entirely. As long as each element (or sublist) matches the shape of the corresponding element in the second list, KDB/Q can seamlessly perform implicit iteration and apply the operator appropriately.

q)(1 2 3;4 5;6 7 8 9)+(10 11 12;50 60;20 30 40 50)
13 15
65
37 48 59

However, if even a single sublist from either list does not match the shape of the corresponding sublist in the second list, the operation will fail, resulting in a length error.

// Note: We removed the atom 50 from the third sublist of our second list
q)(1 2 3;4 5;6 7 8 9)+(10 11 12;50 60;20 30 40)
'length
  [0]  (1 2 3;4 5;6 7 8 9)+(10 11 12;50 60;20 30 40)

The only exception occurs when one of the elements is an atom. In this case, scalar extension is applied, and the atom is automatically extended to match the shape of the corresponding element in the second list.

// Scalar extension applies 
q)(1 2 3;4 5;6 7 8 9)+(10 11 12;50 60;50)
11 13 15
54 65
56 57 58 59

All of this is achieved without writing a single loop - amazing, ins't it? Implicit iteration is a powerful concept that not only makes KDB/Q incredibly fast but also remarkably elegant. For a deeper dive into implicit iteration, be sure to explore Stephen Taylor's detailed post here.

Maps

To ease into the topic, we’ll begin with the simpler of the two categories: Maps. There are six different Map iterators, summarized in the following table

Name	Keyword	Operator	Usage
Each	each	'	v'
Each Left		\:	v2\:
Each Right		/:	v2/:
Each Parallel	peach	':	v1':
Each Prior	prior	':	v2':
Case		'	i'

where

 v1: value (rank 1)
 v2: value (rank 2)
 v : value (rank 1-8)
 i : vector of ints≥0

Each

The each iterator, as the name suggests, allows you to apply a function to each element of a list. This is particularly useful when you want to iterate over a list and perform operations on its individual elements. However, it's important to note that KDB/Q's built-in operators already support implicit scalar iteration, so this functionality is provided natively. As a result, each is most commonly used with custom-defined functions.

Syntax

(v1') x		v1'[x]		v1 each x
v1@'x
x v2 y		v2'[x;y]
		v3'[x;y;z]

The each iterator applies a function item-wise to a dictionary, list, or corresponding items of conforming lists and dictionaries. For example, when v is a function, v' applies v to each item of a list or dictionary, or to matching items from conforming lists. The resulting derived function retains the same rank as v.

This sounds more complicated than it actually is, so let's explorer some practical examples. Let’s start by defining a function f that takes a single argument and returns its square. We can then use the each iterator to apply this function to every element of a list, returning the square of each element.

Unary application of `each`

q)f:{x*x}
q)show list:1+til 10
1 2 3 4 5 6 7 8 9 10
q)f each list
1 4 9 16 25 36 49 64 81 100
// alternative syntax using apply @
q)f@'list
1 4 9 16 25 36 49 64 81 100

Keep in mind that due to implicit scalar iteration, we don’t actually need to use the each iterator to achieve this. Instead, we can simply multiply the two lists directly.

q)1 2 3 4 5 6 7 8 9 10 * 1 2 3 4 5 6 7 8 9 10
1 4 9 16 25 36 49 64 81 100
q)list*list
1 4 9 16 25 36 49 64 81 100

Now, let’s explore a scenario where the we truly need the each iterator. Imagine we have a list of lists, and we want to determine the length of each sublist. Simply applying the count function to the entire list won’t work, as it will only return the count of elements at the top level (depth 1). However, by combining the count operator with the each iterator, we can efficiently calculate the length of each individual sublist at depth 2.

q)count (1 2 3;"Hello World";2025.01.01 2025.01.02; (`AAPL`GOOG;`MSFT))
4
q)count each (1 2 3;"Hello World";2025.01.01 2025.01.02; (`AAPL`GOOG;`MSFT))
3 11 2 2

If you’ve read some of my previous blog posts or aren’t entirely new to KDB/Q, you’ll know that many operators in KDB/Q have multiple overloads or different syntax depending on the function’s arity. The same applies to iterators. Let’s explore the various ways each can be used.

As we've already seen, the task above can be accomplished using the code snippet f each list. Additionally, you can use the following syntax to apply a unary function - a function that takes only one argument - to each element of a list:

// Original solution
q)f each list
1 4 9 16 25 36 49 64 81 100
// More concise and terse solutions
q)f@'list
1 4 9 16 25 36 49 64 81 100
q)(f')list
1 4 9 16 25 36 49 64 81 100

Although there is no significant performance difference between the syntaxes, I strongly recommend using the first syntax, f each list, for better readability. While this example is quite simple and easy to understand, in a larger codebase with more complex logic, the first approach is much clearer and more readable.

q)\ts:1000000 f each list
726 768
q)\ts:1000000 f@'list
781 720
q)\ts:1000000 (f')list
726 688

Binary opplication of `each`

The binary application of each (often called each-both) is used with binary functions, which take two arguments. This usage requires careful attention, as the lengths of the two arguments are crucial. Both lists must have the same length; otherwise, a length error will occur. The only exception is when one of the arguments is an atom instead of a list. In this case, scalar extension will automatically convert the atom into a list of the same length as the other list, as we’ve previously learned. Let’s see how this works in practice.

Imagine we have two lists of strings (recall that a string in KDB/Q is essentially a list of characters), and we want to concatenate their individual elements pairwise. If we use the concatenate operator , alone, it will simply merge the two strings into one. However, by combining the concatenate operator with the each iterator ,' , we can achieve the desired pairwise concatenation.

q)"ABCDE" ,' "12345"
"A1"
"B2"
"C3"
"D4"
"E5"
q),'["ABCDE";"12345"]
"A1"
"B2"
"C3"
"D4"
"E5"
q)(,')["ABCDE";"12345"]
"A1"
"B2"
"C3"
"D4"
"E5"

As noted earlier, if the two lists have differing lengths, a length error will be thrown.

q)"ABCDE" ,' "1234"
'length
  [0]  "ABCDE" ,' "1234"
                ^

Unless one of the lists is a single atom.

q)"ABCDE" ,' "1"
"A1"
"B1"
"C1"
"D1"
"E1"

Varadic application of `each`

Finally, let’s explore the variadic application of the each iterator. As with previous cases, the lengths of the arguments you provide will determine whether the operation succeeds or results in a length error.

// Remember: A string is a char vector
q){x,y,z}'["ABC";"XYZ";"123"]
"AX1"
"BY2"
"CZ3"
q)f:{x+y*z}
q)f'[1 2 3;4 5 6;11 12 13]
45 62 81
// If any of the lists isn't the same length as the others, a length error is thrown
q){x,y,z}'["ABC";"XYZ";"12"]
'length
  [0]  {x,y,z}'["ABC";"XYZ";"12"]
              ^
// However, if any list is a single atom, scalar extension kicks in
// Two lists and an atom
q){x,y,z}'["ABC";"XYZ";"1"]
"AX1"
"BY1"
"CZ1"
// One list and two atoms
q){x,y,z}'["ABC";"X";"1"]
"AX1"
"BX1"
"CX1"

Each-left `\:`

The each-left \: iterator takes a binary function and derives a new binary function that applies the entire right argument to each individual element of the left argument - hence the name "each-left." Qbies often find it challenging to remember whether they’re dealing with each-left or each-right. Here's a simple trick to ensure you'll never forget: pay attention to the direction of the slash. If it’s a backslash \, leaning to the left, you’re using the each-left iterator, meaning the entire list on the right is applied to each element on the left. Conversely, if it’s a forward slash /, leaning to the right, you’re using the each-rigth iterator, which applies the entire left argument to each individual element on the right.

Syntax

Each Left     x v2\: y    v2\:[x;y]   equivalent to -->   v2[;y] each x

Let's have a look at a simple example to demonstrate how each-left works.

q)("Alexander";"Christoph";"Stephan"),\:" lives in London"
"Alexander lives in London"
"Christoph lives in London"
"Stephan lives in London"
q)"ABC",\:"XY"
"AXY"
"BXY"
"CXY"
// Alternative syntax
q),\:["ABC";"XY"]
"AXY"
"BXY"
"CXY"

Using the each-left iterator with a binary function is functionally equivalent to applying a binary function where the second argument y is fixed, and the function iterates over each element of the first argument x, as demonstrated below.

q),\:["ABC";"XY"]
"AXY"
"BXY"
"CXY"
// Fixing the y parameter and using each obtains the same result as using each-left
q),[;"XY"] each "ABC"
"AXY"
"BXY"
"CXY"

Each-Right `/:`

The each-righht /: iterator is kind of the counter part to the each-left iterator. The each-right iterator takes a binary function and derives a new binary function that applies the entire left argument to each individual element of the right argument - hence the name each-right.

Syntax

Each Right    x v2/: y    v2/:[x;y]   equivalent to -->   v2[x;] each y

If you've understood the concept of each-left, understanding the workings of each-right should be relatively straightforward. However, for the sake of completeness, let's explore a few illustrative examples.

q)"My name is ",/:("Alexander";"Christoph";"Stephan")
"My name is Alexander"
"My name is Christoph"
"My name is Stephan"
q)"ABC",/:"XY"
"ABCX"
"ABCY"
// Alternative syntax
q),/:["ABC";"XY"]
"ABCX"
"ABCY"

Using the each-right iterator with a binary function is functionally equivalent to applying a binary function where the first argument x is fixed, and the function iterates over each element of the second argument y, as demonstrated below:

q),/:["ABC";"XY"]
"ABCX"
"ABCY"
q),["ABC";] each "XY"
"ABCX"
"ABCY"

Each Parallel

The iterator each-parallel ': - or its corresponding keyword peach - enables parallel execution by delegating processing to secondary tasks. This is particularly useful for computationally intensive functions or scenarios requiring simultaneous access to multiple drives from a single CPU.

To enable parallel execution, start KDB/Q with multiple secondary processes using the -s option in the command line. The each-parallel iterator gains a performance improvement by dividing the argument list of the derived function among the available secondary processes for evaluation. The result of applying each-parallel to a unary function will always match the result of applying each to the same function, meaning m':[x] will always be identical to m'[x]. However, each-parallel offers a performance advantage over each when secondary tasks are available. If no secondary tasks are available, the performance will remain the same as that of each.

Syntax

(v1':)x   v1':[x]   v1 peach x

Let's illustrate the performance advantage of peach:

// First, we start KDB/Q with secondary threads, in this case 4
KDB+ 4.0 2023.01.20 Copyright (C) 1993-2023 Kx Systems
m64/ 8(24)core 24576MB alexanderunterrainer mac EXPIRE 2025.02.21 KDB PLUS TRIAL #5018719
// You can verify the number of available threads using the \s command
q)\s
4i
// Generate a vector with one million numbers and square each element using the peach iterator
q)r_peach:{x*x} peach til 1000000
// Generate a vector with one million numbers and square each element using the each iterator
q)r_each:{x*x} each til 1000000
// Verify that the result matches
q)r_peach~r_each
1b
// time the same operation using 100 million numbers
q)\ts {x*x} peach til 100000000
5692 4294967888
q)\ts {x*x} each til 100000000
7188 4821226064

tip

To start a KDB/Q process with secondary threads, use the -s n command line option. You can check the number of available secondary threads within a KDB/Q process by running the \s command.

As you can see from the above results, using peach to compute the square of one hundred million numbers results in approximately 30% faster execution time compared to using the each iterator. Moreover, peach consumes around 13% less memory than each.

While incorporating peach into your code can offer clear performance benefits over the standard each iterator, it does come with certain limitations. For example, only the main thread can update global variables. As a result, you need to carefully assess whether peach and parallel processing are the right fit for your application.

Each Prior

The each-prior ': iterator - or its coresponding keyword prior - applies a binary function between each element of a list and its preceding element. More precisely, each-prior takes a binary function and derives a variadic function that evaluates the function between each item in a list or dictionary and the item that precedes it.

Syntax

(v2':)x    v2':[x]      (v2)prior x
x v2':y    v2':[x;y]

This might sound more complex than it actually is, so let’s explore an example to help clarify how each-prior works:

q)(-':)100 99 101 105 100 120
100 -1 2 4 -5 20

Looking at the result of the above computation, you'll notice that the first element of the result vector stands out. This is because the initial item in the list has no predecessor, so KDB/Q implicitly selects the identity value for the binary function (if one exists).

note

The identity value for addition + and subtraction - is 0, whereas for multiplication * and division % it is 1.

Alternatively, we can specify the initial value to be used as the predecessor by applying it as the left operand of the modified operator. A common choice is to use the first item of the source list. For instance, this approach can be used to calculate the deltas of a list of prices.

q)100 -': 100 99 101 105 100 120
0 -1 2 4 -5 20

If you're curious about practical applications of the each-prior iterator, you might be surprised to learn that it is more commonly used than you might expect. In fact, each-prior serves as the foundation for the underlying implementation of keywords like deltas, ratios and differ. Let me take you behind the scenes to show how it works.

q)deltas
-':
q)ratios
%':
q)differ
$["b"]~~':

When using deltas without explicitly providing an initial value as the predecessor for the first element of the list, we observe the same behavior we encountered earlier - he first element of the result may not align with our expectations. However, by understanding how to explicitly supply an initial value and slightly modifying the underlying definition of the deltas keyword, we can create our own customized delta function. Let’s do that!

q){first[x]-':x} 100 99 101 105 100 120
0 -1 2 4 -5 20
q)mydeltas:{first[x]-':x}
q)mydeltas 100 99 101 105 100 120
0 -1 2 4 -5 20

You can also use the prior keyword to improve readability.

q)prior
k){x':y}
q)(-) prior 100 99 101 105 100 120
100 -1 2 4 -5 20

Case

The final map iterator we’ll explore is the case iterator. To be completely honest, I’ve never actually used it in practice - o if you ever come across a real-world use case (pun intended), feel free to share it with me! Now, back to iterators: The case iterator selects successive items from multiple list arguments, with the left argument of the iterator determining which argument each item is picked from.

Syntax

int'[a;b;c;…]

where

int is an integer vector
[a;b;c;…] are the arguments to the derived function

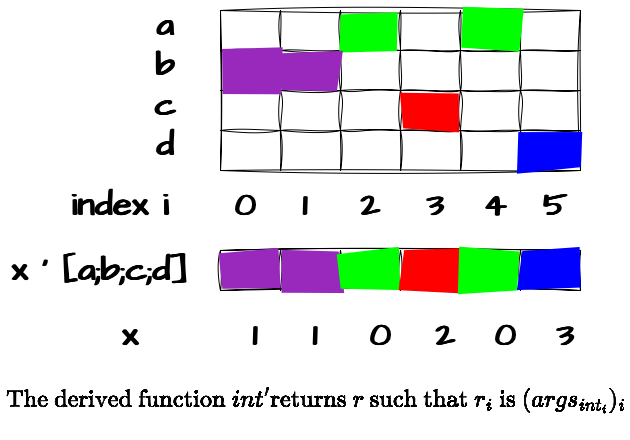
Case Syntax

The best way to understand the case iterator is through an example. Imagine you have a list of different languages - German, Italian, French, and English - and you want to print the numbers one to six, switching languages in a specific order: German, German, Italian, French, Italian, and English. The case iterator makes this task effortless. Let’s see it in action.

We first define a list of avaialble languages, and store them in a variable

q)language:`Italian`German`French`English

Next, we have to define the numbers from one to six in each language:

q)e:`one`two`three`four`five`six
q)g:`eins`zwei`drei`vier`funf`sechs
q)f:`un`deux`trois`quatre`cinq`sees
q)i:`uno`due`tre`quattro`cinque`sei

We can use the find operator ? to generate a vector of indices that map to the desired sequence of languages for displaying the numbers. This approach is similar to creating an enumeration (which we will explore in a separate blog post). Let me illustrate the concept.

q)language?`German`German`Italian`French`Italian`English
1 1 0 2 0 3

Finally, we can use this index vector in combination with the case iterator to cycle through the different languages and select the correct word for each number. Since we aim to display six numbers, our index vector has a length of six. Starting with the first index (0), the value at this position is 1, meaning we will take the word at index 0 from the language list located at index 1. Mind-bending, right? As always, the best way to understand this concept is through an example. After all, a single line of KDB/Q code speaks louder than a million words!

q)(language?`German`German`Italian`French`Italian`English)'[i;g;f;e]
`eins`zwei`tre`quatre`cinque`six
q)1 1 0 2 0 3'[i;g;f;e]
`eins`zwei`tre`quatre`cinque`six

Let's break it down even further and walk through it step by step:

First, note that our argument list is [i;g;f;e], representing the list of numbers in different languages: Italian, German, French, and English. The key detail here is the index positions: Italian is at index 0, German at index 1, French at index 2, and English at index 3.

Now, we map the index of each language to the desired order in which we want the words to appear—German, German, Italian, French, Italian, and English—resulting in the following vector:1 1 0 2 0 3.

The final output, eins, zwei, tre, quatre, cinque, six is derived as follows:

eins: We first index into our language list at position 1 (German vector), then index into it at position 0, returning eins.
zwei: Again, we access index 1 (German vector) and this time retrieve index 1, yielding zwei
tre: Moving to index 0 (Italian vector), we select index 2, which gives tre
quatre: Next, at index 2 (French vector), we fetch index 3, producing quatre.
cinque: Returning to index 0 (Italian vector), we retrieve index 4, yielding cinque
six: Finally, at index 3 (English vector), we select index 5, resulting in six

By following this pattern, we traverse the entire index vector and achieve the intended sequence of translated numbers.

With this, we wrap up the Map Iterators and can now move on to the Accumulator Iterators: Scan \ and Over /.

Accumulators

Every KDB/Q developer knows that mastering Iterator - especially Scan and Over - sets apart an experienced developer from a Qbie (beginner). While similar concepts exist in other programming languages, such as Map and Fold, the syntax of Scan and Over is quite unique and can take time to fully internalize. Moreover, the various overloads of these Iterators, depending on the arity of the function they are applied to, add another layer of complexity to understanding these powerful tools.

In this section, my goal is to help you understand Scan and Over more intuitively. Let's begin with an overview of their syntax and various overloads.

Name	Syntax 1	Syntax 2	Syntax 3
Converge	`(v1\)x`	`v1\[x]`	`v1 scan x`
	`(v1/)x`	`v1/[x]`	`v1 over x`
Do	`n v1\x`	`v1\[n;x]`
	`n v1/x`	`v1/[n;x]`
While	`t v1\x`	`v1\[t;x]`
	`t v1/x`	`v1/[t;x]`
Scan	`(v2\)x`	`v2\[x]`	`(v2)scan x`
Over	`(v2/)x`	`v2/[x]`	`(v2)over x`
Scan	`x v2\y`	`v2\[x;y]`
Over	`x v2/y`	`v2/[x;y]`
Scan	`v3\[x;y;z]`	`x y\z`
Over	`v3/[x;y;z]`

where

v1,v2,v3 are applicable values of rank 1 to 3, respectively
n is an interger greater or equal to 0 (≥0)
t is an unary truth map, basically a truth condition
x,y are the arguments/indexes of v

An accumulator is an iterator that takes an applicable value as an argument and derives a function that evaluates this value - first on its entire (first) argument, then on the results of successive evaluations. The two iterators, Scan and Over, share the same syntax and perform identical computations. However, while Scan-derived functions return the result of each evaluation step, Over-derived functions return only the final result. The Scan and Over iterators are higher-order functions that serve as the primary mechanism for recursion in KDB/Q. In their simplest form, they modify a binary function to accumulate results over a list.

In many ways, Over is similar to map-reduce in other programming languages.

note

While Scan and Over perform the same computation, in general, Over requires less memory, because it does not store intermediate results.

Scan `\` and Over `/`

Since Scan \ and Over / share the same syntax and perform the same computation, with the only difference that Scan returns all intermediate accumulations while Over returns only the final result, we will explore both iterators together, providing examples for each.

Unary functions

The first application of Scan and Over we will explore is their combination with a unary function. Depending on the syntax and arguments used, this can result in three distinct behaviors: Converge, Do, or While. In the following sections, we will learn about each of these behaviors in detail.

Converge

Scan (v1\)x
Over (v1/)x		runs until two successive evaluations match, or an evaluation matches x

When applying Scan or Over to a unary function, a function that takes a single argument, the iterator recursively applies the function, starting from the base case, until the output converges or a loop is detected. Wondering how convergence is determined? At each step, the result is compared to the previous step. If the two values match within an equality tolerance (10⁻¹⁴ at the time of writing), the algorithm is considered to have converged, and recursion stops; otherwise, it continues. Let's illustrate this behavior.

Assume we want to repeatedly multiply a given number by 0.1 until the result matches its predecessor within the specified equality tolerance. We can achieve this using the following code.

Convergence using Scan, printing all intermediate steps
q){x*0.1}\[1]
1
0.1
0.01
0.001
0.0001
1e-05
1e-06
1e-07
1e-08
1e-09
1e-10
1e-11
1e-12
1e-13
1e-14
1e-15
1e-16
1e-17
1e-18
1e-19
1e-20
1e-21
..
q)count {x*0.1}\[1]
309
// Convergence using Over returns the last value before the recursion terminated
q){x*0.1}/[1]
0f
// the last result of Scan matches the result of Over 
q){x*0.1}/[1]~last {x*0.1}\[1]
1b

Since Over only returns the final result before convergence, we use Scan to visualize the intermediate steps. As seen in the example above, it took 309 iterations for the results to fall within the equality tolerance, at which point convergence was achieved, and the recursion terminated.

The second condition for KDB/Q to terminate recursion is when it detects a loop, meaning the result of an evaluation matches the initial input. Without this safeguard, the process would run indefinitely. The following two examples demonstrate how loop detection works.

First, we use the neg operator to negate the input, producing its negative counterpart. On the second iteration, negating the result again returns the original value, detecting a loop and terminating the recursion.

q)(neg\)1
1 -1

In the second example, we use the rotate operator to shift a given string (a vector of characters) by one position at a time. Repeating this process eventually brings the string back to its original form, at which point the recursion halts.

q)1 rotate "Hello"
"elloH"
q)rotate[1;"Hello"]
"elloH"
q)(rotate[1]\)"Hello"
"Hello"
"elloH"
"lloHe"
"loHel"
"oHell"

However, despite all these built-in safeguards, it’s still possible to create an infinite loop. One simple way to do so is by understanding how not behaves in KDB/Q. In standard Boolean logic, not simply flips the input: 0b (false) becomes 1b (true) and vice versa. But in KDB/Q, not returns 0b when the input is nonzero and 1b otherwise.

This means that if we use not with Scan \ or Over /, starting with any value other than 0 or 1, we will enter an infinite loop. Applying not to any nonzero number yields 0b, and applying not to 0b returns 1b. Since 0 will never match 1, convergence never occurs. Likewise, because our starting input wasn’t 1, a loop is never detected, trapping us in an endless cycle.

danger

DO NOT RUN BELOW!! You will have to kill your console session if you enter the following code

q)not 0
1b
q)not 1b
0b
q)not 2
0b
// This will never retunr
q)(not/) 42 

Do

i v1\x
i v1/x		i, a non-negative integer

Using Scan \ or Over / with a unary function and a non-negative integer effectively mimics a Do loop, where the integer specifies the number of iterations, and the right operand serves as the initial value. Leveraging this, we can easily construct a loop that increments a starting value by 1, ten times.

// Using Scan to add 1 to 10, 10 times
q)10{x+1}\10
10 11 12 13 14 15 16 17 18 19 20
// Over returns only the last result
q)10{x+1}/10
20

We can leverage this knowledge to create a pattern I was first introduced by Stephen Taylor. Suppose you want to write a function to identify palindromes, a word, phrase, or sequence that reads the same backwards as forwards. This can be efficiently achieved by combining the reverse operator with Scan, applying the function exactly once. Since Scan outputs the original input as the first result when used in combination with a unary function, you can then compare it with the reversed version and determine whether the two match, indicating a palindrome.

q)1 reverse\"anna"
"anna"
"anna"
q)(~) . 1 reverse\"anna"
1b
q)(~) . 1 reverse\"annA"
0b

note

Only when used with a unary function, Scan returns the initial argument.

While

t v1\x
t v1/x		until unary value t, evaluated on the result, returns 0

The last unary overload of Scan \ or Over / is equivalent to a "while" loop in imperative programming. It offers a declarative way to define a termination condition for the iteration. The process continues as long as the predicate evaluates to 1b and stops otherwise. For instance, we can repeatedly multiply a number by 2 while the result remains less than 100 or square a given input until the result exceeds 1000.

q)(100>){2*x}\2
2 4 8 16 32 64 128
q)(<1000){x*x}\2
'<
  [0]  (<1000){x*x}\2
        ^
q){x<1000}{x*x}\2
2 4 16 256 65536

Notice how the second attempt in the code above results in an error? You can prevent this by converting the test condition into a lambda and explicitly defining x within it.

q)(10>)4
1b
q)(<10)4
'<
  [0]  (<10)4
        ^
q){10>x}4
1b
q){x<10}4
1b
q){x<1000}{x*x}\2
2 4 16 256 65536
q){100>x}{2*x}\2
2 4 8 16 32 64 128

Binary functions

When applying the Scan \ or Over / iterator to a binary function, it derives a function that first evaluates the value on its entire (first) argument and then on the results of successive evaluations. The number of evaluations corresponds to the count of the right argument.

Binary application

Scan      x v2\y    v2\[x;y]
Over      x v2/y    v2/[x;y]

For example, suppose we want to sum the first 10 natural numbers starting from 1. In imperative programming, this would require control flow: initializing a result variable, setting up a loop counter, and iterating while adding to the result until the counter reaches the end of the list.

In KDB/Q, however, you can simply accumulate values, starting with an initial accumulator. There are no counters, no tests, and no explicit loops! Using the binary overload of Scan \ or Over /, the initial accumulator value is the left operand, and the list to accumulate over is the right operand. Internally, each item of the list is progressively added to the accumulator, moving through the list until completion. The final accumulated value is then returned.

For instance, with an initial accumulator value of 0:

1 is added to 0, resulting in 1
2 is then added to 1, yielding 3
This process continues until the end of the list

This operates just like traditional imperative code, but without explicit control structures.

q)0+\1 2 3 4 5 6 7 8 9
1 3 6 10 15 21 28 36 45
q)0+/1 2 3 4 5 6 7 8 9
45

tip

You can use 0N! to examine what is happening behind the curtains

q)0 {0N!(x;y); x+y}/ 1 2 3 4 5
0 1
1 2
3 3
6 4
10 5
15
q)0+/1 2 3 4 5
15

This pattern of combining Scan or Over with a binary function is so powerful that several keywords leverage it behind the scenes. Here are some of them:

q)sum 1 2 3 4
10
q)(+/)1 2 3 4
10
q)sums
+\
q)sums 1 2 3 4
1 3 6 10
q)(+\)1 2 3 4
1 3 6 10
q)prd 1 2 3 4
24
q)(*/)1 2 3 4
24
q)prds
*\
q)(*\)1 2 3 4
1 2 6 24
q)min 1 2 3 4
1
q)(&/)1 2 3 4
1
q)mins
&\
q)(&\)1 2 3 4
1 1 1 1
q)max 1 2 3 4
4
q)(|/)1 2 3 4
4
q)maxs
|\
q)(|\)1 2 3 4
1 2 3 4

Unary application

Although applying a binary function in a unary context might seem counterintuitive, in many cases, explicitly specifying the initial accumulator value is unnecessary.

For instance, in our summation example, instead of providing an initial accumulator, we can simply start with the first item in the list and accumulate the remaining values. This is achieved by enclosing the modified function in parentheses and omitting the initial accumulator:

q)(+\) 1 2 3 4 5 6 7 8 9 10
1 3 6 10 15 21 28 36 45 55
q)(+/) 1 2 3 4 5 6 7 8 9 10
55

Conceptually, you can think of the list in its general form:

q)(1; 2; 3; 4; 5; 6; 7; 8; 9; 10)
1 2 3 4 5 6 7 8 9 10
q)1+til 10
1 2 3 4 5 6 7 8 9 10
q)(1; 2; 3; 4; 5; 6; 7; 8; 9; 10)~1+til 10
1b
q)(1 2 3 4 5 6 7 8 9 10)~(1; 2; 3; 4; 5; 6; 7; 8; 9; 10)
1b

Using (+/) effectively replaces the semicolons ; with a plus +, associating the operation from the left.

A few key points about this form:

The parentheses are necessary
The modified function is now unary.
This code is actually k code rather than KDB/Q - so you're technically writing k code (Don't tell anyone!)

Moreover, both, the unary and binary from of Scan \ and Over / can also be written in prefix notation

q)+/[0; 1 2 3 4 5 6 7 8 9 10]
55
q)+\[0; 1 2 3 4 5 6 7 8 9 10]
1 3 6 10 15 21 28 36 45 55
q)+/[1 2 3 4 5 6 7 8 9 10]
55
q)+\[1 2 3 4 5 6 7 8 9 10]
1 3 6 10 15 21 28 36 45 55

The keywords `scan` and `over`

You can use the scan and over keywords to apply a binary function to a list or dictionary. However, if you are using an infix function as the left argument, make sure to enclose it in parentheses.

q)(+) scan 1 2 3 4
1 3 6 10
q)(+) over 1 2 3 4
10
q)show d:`a`b`c`d!`b`d`c`a
a| b
b| d
c| c
d| a
q)d scan `a
`a`b`d
q)d over `b
`a
q)d scan `b
`b`d`a

Ternary functions

Finally, let's examine the combination of iterators with ternary functions (functions that take three arguments) or functions of even higher arity (up to eight arguments). When an accumulator derives a function from an initial function with a rank greater than two, it retains the same rank as the original function. Functions derived using Scan \ are uniform, while those derived using Over / are aggregates. The number of evaluations corresponds to the maximum count of the right arguments.

For v\[x;y;z] and v/[x;y;z]:

x is the initial argurment, and belongs to the left domain of v
y and z are either atoms, conforming lists, or dictionaries within the right domains of v
The first evaluation is v[x; first y; first z], and its result becomes the left argument for the next evaluation, continuing in this manner.

For example, for r:v\[x;y;z], the iterative process applies the function across the provided arguments accordingly.

r[0]: v[x  ; y 0; z 0]
r[1]: v[r 0; y 1; z 1]
r[2]: v[r 1; y 2; z 2]
…

The result of v/[x;y;z] is simply the last item of the above

v/[x;y;z]
v[ v[… v[ v[x;y0;z0] ;y1;z1]; … yn-2;zn-2]; yn-1;zn-1]

Here are some examples to help you get familiar with this syntax and concept.

q){x+y*z}\[1000;5 10 15 20;2 3 4 5]
1040 1100 1200
q){x+y*z}\[1000 2000;5 10 15 20;3]
2015
2045
2090
2150

But what about a more practical example? Imagine you're working at a large corporation with hundreds of processes running across multiple regions, each with several instances. Your team follows a naming convention: "ProcessName.Region_InstanceNumber", such as "ProcessName.Region_InstanceNumber". Your task is to extract the region from a given process name. While this might seem trivial, you'd be surprised how tricky it can be in many mainstream programming languages. However, in KDB/Q, it's just a one-liner! By combining the Over iterator / with the vs,first, and last operators, we can easily achieve this. Let's try it!

q){z y vs x}/["TICKERPLANT.US_1";"._";(last;first)]
"US"

Magic? Not quite—but close! Here's what's happening:

The input "TICKERPLANT.US_1" is passed as x to our lambda {z y vs x}, along with the first item of y, which is ".", and the first item of z, which is the last operator. This results in the expression:

last "." vs "TICKERPLANT.US_1"

which evaluates to "US_1". This intermediate result is then passed as x into the next iteration of our lambda, where y is "_" and z is first, forming:

first "_" vs "US_1"

which returns the final result: "US". In theory, you could achieve the same result with:

q)first "_" vs last "." vs "TICKERPLANT.US_1"
"US"

but it's nowhere near as elegant as our approach using Over.

This concludes our section on Scan \ and Over /. Take a moment to review their various overloads, syntax, and the different behaviors they exhibit based on function arity and the number of parameters.

Combining Iterators

The power of Iterators extends beyond their individual applications - you can also combine them to create even more efficient and powerful code. In the next section, we will explore two examples that demonstrate how iterators can be used in combination.

For our first example, let's say you have two lists of numbers and want to determine all possible ways to pair their elements. This is essentially finding the permutations of two sets, a common problem in mathematics. While it’s easy to do manually with pen and paper, implementing it in code can be less straightforward.

Consider the list 1 2 3, and suppose we want to generate all possible pairs of these numbers with themselves. Our two lists are 1 2 3 and 1 2 3. The expected output would be:

(1,1), (1,2), (1,3)
(2,1), (2,2), (2,3)
(3,1), (3,2), (3,3)

Seems simple, right? But how would you implement this? Combining two iterators, the each-right /: and the each-left \: iterators, this task becomes a simple, concise KDB/Q one-liner. Let's take a look at how this works:

q)1 2 3 ,/:\:1 2 3
1 1 2 1 3
1 2 2 2 3
1 3 2 3 3

If the output doesn’t look as expected because you anticipated a list of pairs, let’s take a closer look at the actual structure. We can use the 0N! operator to inspect the underlying data format. Doing so reveals that the output is, in fact, a list of lists, or more precisely, a list of pairs (tuples).

q)0N!1 2 3 ,/:\:1 2 3
((1 1;1 2;1 3);(2 1;2 2;2 3);(3 1;3 2;3 3))
1 1 1 2 1 3
2 1 2 2 2 3
3 1 3 2 3 3

We can now apply the raze operator to flatten one level of nesting in our result, giving us the exact output we expect.

q)raze 1 2 3 ,/:\:1 2 3
1
2
3
1
2
3
1
2
3
q)0N!raze 1 2 3 ,/:\:1 2 3
(1 1;1 2;1 3;2 1;2 2;2 3;3 1;3 2;3 3)
1
2
3
1
2
3
1
2
3

Our next example builds on the previous one as we take a deeper look at the raze operator. If we examine how raze is defined under the hood, we see that it’s simply a combination of the concatenate operator , and the Over / iterator.

q)raze
,/

This makes sense because flattening one level of nesting is essentially just joining or concatenating the nested lists at that level. But what if the nesting goes deeper, spanning multiple levels? This is where combining iterators comes in handy to achieve full flattening across all levels. By applying raze with Over, essentially using Over twice, we can completely eliminate all layers of nesting.

// Create a list with several layers of nesting
q)(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1
(1 2;(1 2 3;4 5);(10 12;13 14))
(((3 4;5 6);(10 20 30;40 50));(1 2;3 4))
// Applying raze only eliminates one level of nesting 
q)raze (1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1
1 2
(1 2 3;4 5)
(10 12;13 14)
((3 4;5 6);(10 20 30;40 50))
(1 2;3 4)
// However, combining raze with over will eliminate all layers of nesting
q)raze/[(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))]
1 1 2 1 2 3 4 5 10 12 13 14 3 4 5 6 10 20 30 40 50 1 2 3 4

tip

If you want even more concise and elegant code, you can take advantage of raze's underlying definition and combine it with Over to create the terse expression (,//)x, which achieves the same result as raze/[x]. However, keep in mind that this is k code rather than q.

q)(,//)(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1 1 2 1 2 3 4 5 10 12 13 14 3 4 5 6 10 20 30 40 50 1 2 3 4

But why stop here? You can take it a step further and create a modified version of raze hat allows you to control how many levels of nesting you want to flatten. Shortly after I published the initial version of this blog post, none other than Charles Skelton, former CTO and now Chief Scientist at KX, suggested this addition. The elegant snippet n,//x lets you flatten a nested list n times. And that’s exactly what I aim for with DefconQ, to foster a collaborative space where KDB/Q developers can learn and grow together!

q)3,//(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1
1
2
1
2
3
4
5
10
12
13
14
3 4
5 6
10 20 30
40 50
1
2
3
4
q)2,//(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1
1
2
1 2 3
4 5
10 12
13 14
(3 4;5 6)
(10 20 30;40 50)
1 2
3 4
q)1,//(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1
1 2
(1 2 3;4 5)
(10 12;13 14)
((3 4;5 6);(10 20 30;40 50))
(1 2;3 4)
q)4,//(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))
1 1 2 1 2 3 4 5 10 12 13 14 3 4 5 6 10 20 30 40 50 1 2 3 4
q),//[2;(1; (1 2;(1 2 3;4 5);(10 12;13 14));(((3 4;5 6);(10 20 30;40 50));(1 2;3 4)))]
1
1
2
1 2 3
4 5
10 12
13 14
(3 4;5 6)
(10 20 30;40 50)
1 2
3 4

Tips and Tricks

We've now covered all the Iterators, their syntax, overloads, behaviors, and functionality. Most of the content in this blog post is not new and has been documented on code.kx.com. However, in this section, I'd like to share a few tips and tricks.

How to know which iterator is used

The first question, identifying which Iterator is used in a given piece of code, is relatively straightforward: simply look at the operator. It should be easy to distinguish between Each ' (each), Each-Left \:, and 8Each-Right* /: (remember, you can tell Each-left from Each-right based on which direction the slash leans), as well as Scan \ and Over /.

Where things get trickier is distinguishing between Each-both ', Each-Prior ':, Each-Parallel ':, or determining which overload of Scan and Over is being used. In these cases, your next step should be to examine the arity of the function the Iterator is applied to: how many arguments it takes and how many are being passed.

If a unary function is used, Scan and Over can exhibit three different behaviors: Converge, Do, or While. This depends on the number and type of parameters passed:

Converge: No parameter is passed.
Do: The x argument is a positive integer.
While: The first argument x is a true condition.

Following this approach will help you understand what’s really happening in the code. Additionally, it's always a good idea to have a KDB/Q console open so you can test snippets and observe their behavior firsthand.

How to understand what's happening

If you're still struggling to understand what's happening, don’t panic. Take a deep breath and take a step back.

If you're using the Over / iterator and can't quite understand how the final result was achieved, try replacing Over / with Scan \. This will display all the intermediate steps, which might help you spot a pattern and better understand the process. Seeing the full sequence of calculations can often make things clearer.

For any other Iterator, or really any piece of code, use 0N! to print to the console. It's one of the fundamental debugging techniques: print out values to see what’s going on under the hood.

q){0N!(x;y);x,y}/:\:[1 2 3;4 5 6]
4
5
6
4
5
6
4
5
6
4 1 5 1 6
4 2 5 2 6
4 3 5 3 6
q)1 2 3,/:\:4 5 6
4 1 5 1 6
4 2 5 2 6
4 3 5 3 6

That wraps up our session on Iterators. I hope you found it helpful and enjoyable! If you did, feel free to follow me and DefconQ on LinkedIn and subscribe to my free newsletter to stay updated with my latest blog posts and get updates straight to your inbox.

Until next time - happy coding!

Resources:

Iterators: Navigating Vectors Without the Need for Loops

Why we use Iterators​

Implicit Iteration​

Maps​

Each​

Syntax​

Unary application of each​

Binary opplication of each​

Varadic application of each​

Each-left \:​

Syntax​

Each-Right /:​

Syntax​

Each Parallel​

Syntax​

Each Prior​

Syntax​

Case​

Syntax​

Accumulators​

Scan \ and Over /​

Unary functions​

Converge​

Do​

While​

Binary functions​

Binary application​

Unary application​

The keywords scan and over​

Ternary functions​

Combining Iterators​

Tips and Tricks​

How to know which iterator is used​

How to understand what's happening​

Why we use Iterators

Implicit Iteration

Maps

Each

Syntax

Unary application of `each`

Binary opplication of `each`

Varadic application of `each`

Each-left `\:`

Syntax

Each-Right `/:`

Syntax

Each Parallel

Syntax

Each Prior

Syntax

Case

Syntax

Accumulators

Scan `\` and Over `/`

Unary functions

Converge

Do

While

Binary functions

Binary application

Unary application

The keywords `scan` and `over`

Ternary functions

Combining Iterators

Tips and Tricks

How to know which iterator is used

How to understand what's happening